Embark on an exploration of the surface areas of pyramids and cones, geometric forms with intriguing properties and practical applications. From their distinct shapes to their intricate formulas, we delve into the captivating world of these three-dimensional objects.
In this comprehensive guide, we will unravel the mysteries of pyramids and cones, examining their types, unraveling the formulas used to calculate their surface areas, and exploring the diverse fields where these formulas find practical application. Prepare to be captivated as we uncover the relationships between surface area and volume, delve into the intricacies of truncated pyramids and cones, and answer commonly asked questions about these fascinating shapes.
Types of Pyramids and Cones

Pyramids and cones are two types of three-dimensional shapes that share a common base and a single vertex.
Types of Pyramids, Surface areas of pyramids and cones
| Type | Base Shape | Number of Lateral Faces | Number of Vertices |
|---|---|---|---|
| Regular Pyramid | Regular polygon | Number of sides of base | Number of sides of base + 1 |
| Triangular Pyramid | Triangle | 3 | 4 |
| Square Pyramid | Square | 4 | 5 |
| Pentagonal Pyramid | Pentagon | 5 | 6 |
Types of Cones
| Type | Base Shape | Number of Lateral Faces | Number of Vertices |
|---|---|---|---|
| Circular Cone | Circle | 1 | 2 |
| Elliptical Cone | Ellipse | 1 | 2 |
| Parabolic Cone | Parabola | 1 | 2 |
| Hyperbolic Cone | Hyperbola | 1 | 2 |
Surface Area Formulas
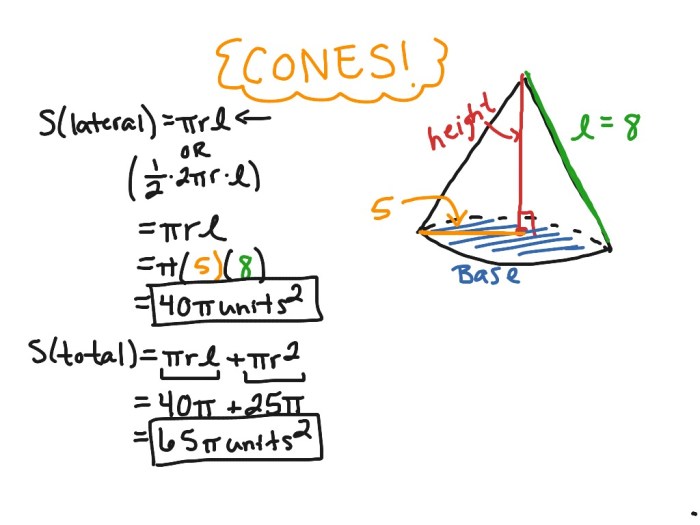
The surface area of a pyramid or cone is the sum of the areas of its base and lateral faces.
Pyramids
- Surface Area = Base Area + (1/2) – Perimeter of Base – Slant Height
Cones
- Surface Area = Base Area + (1/2) – Circumference of Base – Slant Height
Steps to Use the Formulas:
- Calculate the area of the base using the appropriate formula (e.g., area of a circle, triangle, square).
- Find the perimeter or circumference of the base.
- Determine the slant height (the distance from the vertex to the midpoint of a side of the base).
- Substitute the values into the surface area formula.
Applications of Surface Area
The surface area of pyramids and cones is used in various fields, including:
- Architecture:Calculating the surface area of roofs, walls, and other structures.
- Engineering:Determining the surface area of tanks, silos, and other containers.
- Medicine:Estimating the surface area of organs and implants.
- Manufacturing:Calculating the surface area of packaging materials and other products.
Relationships Between Surface Area and Volume
The surface area and volume of pyramids and cones are related in the following ways:
- For a given volume, a pyramid or cone with a smaller surface area will be more efficient in terms of space utilization.
- For a given surface area, a pyramid or cone with a larger volume will be more efficient in terms of storage capacity.
Example:Consider two pyramids with the same base area and slant height. If one pyramid has a square base and the other has a triangular base, the square-based pyramid will have a smaller surface area but a larger volume.
Surface Area of Truncated Pyramids and Cones: Surface Areas Of Pyramids And Cones

A truncated pyramid or cone is a shape that results from cutting off the top of a regular pyramid or cone by a plane parallel to the base.
Truncated Pyramid
- Surface Area = Base Area + Top Area + (1/2) – Perimeter of Base – Slant Height
Truncated Cone
- Surface Area = Base Area + Top Area + (1/2) – Circumference of Base – Slant Height
Example:A truncated cone with a circular base has a base radius of 5 cm, a top radius of 3 cm, and a slant height of 10 cm. The surface area of the cone is:
- Surface Area = (π – 5^2) + (π – 3^2) + (1/2) – (2π – 5) – 10 = 142.69 cm 2
Popular Questions
What is the formula for calculating the surface area of a pyramid?
The surface area of a pyramid is given by the formula: SA = B + 1/2 – P – l, where B is the area of the base, P is the perimeter of the base, and l is the slant height (the height of the triangular faces).
How do I calculate the surface area of a truncated pyramid?
To calculate the surface area of a truncated pyramid, use the formula: SA = B1 + B2 + P – l, where B1 and B2 are the areas of the upper and lower bases, P is the perimeter of the base, and l is the slant height (the height of the lateral faces).
What is the relationship between the surface area and volume of a pyramid?
The surface area and volume of a pyramid are related by the formula: V = 1/3 – B – h, where V is the volume, B is the area of the base, and h is the height of the pyramid.